This post was inspired by an article on the BBC website by Martin Rosenbaum, which presented data on a localised breakdown of EU referendum voting figures, and a subsequent discussion of those results in a Facebook group. In that discussion, I observed that the negative correlation between the percentage of graduates in an electoral ward and the leave vote in that ward was remarkable, and much higher than any correlation you normally see in the social sciences. My friend Barry observed that age was also correlated with voting leave, and that it was likely that age would be correlated with the percentage of graduates, and questioned whether the percentage of graduates was really an independent predictor, or whether a high percentage of graduates was more a marker for a young population.
The BBC article, fascinating though it is, didn’t really present its findings in enough detail to be able to answer that question. Happily, Rosenbaum made his raw data on voting results available, and data on age and education are readily downloadable from the Nomis website, so I was able to run the analysis myself to investigate.
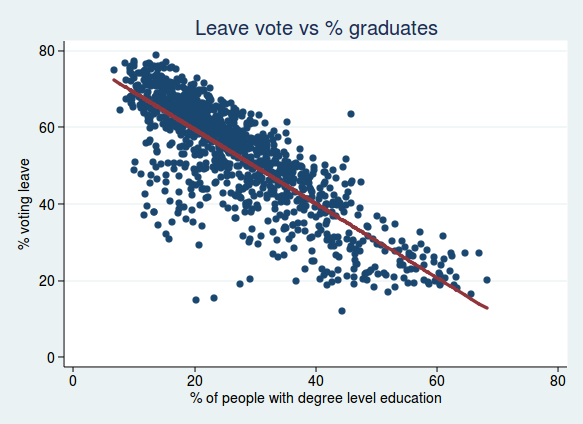
To start with, I ran the same analyses as described in Rosenbaum’s article, and I’m happy to say I got the same results. Here is the correlation between voting leave and the percentage of graduates, together with a best-fit regression line:
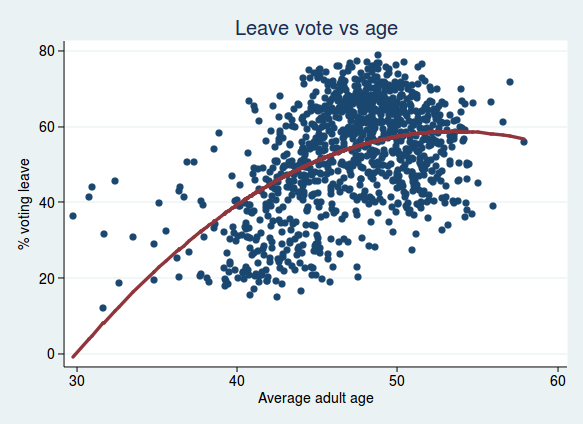
For age, I found that adding a quadratic term improved the regression model, so the relationship between age and voting leave is curved, and increases with age at first, but tails off at older age groups:
Rosenbaum also looked at the relationship with ethnicity, so I did too. Here I plot the percent voting leave against the % of people in each ward identifying as white. Again, I found the model was improved by a quadratic term, showing that the relationship is non linear. This fits with what Rosenbaum said in his article, namely that although populations with more white people were mostly more likely to vote leave, that relationship breaks down in populations with particularly high numbers of ethnic minorities:
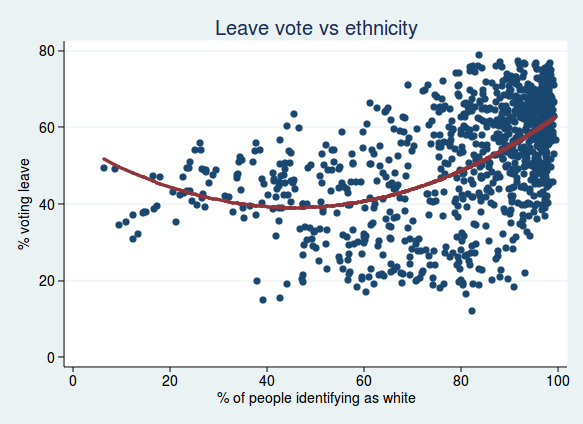
It’s interesting to note that the minimum for the % voting leave is a little over 40% white population. I suspect that the important thing here is not so much what the proportion of white people is, but how diverse a population is. Once the proportion of white people becomes very low, then maybe the population is just as lacking in diversity as populations where the proportion of white people is very high.
Anyway, the question I was interested in at the start was whether the percentage of graduates was an independent predictor of voting, even after taking account of age.
The short answer is yes, it is.
Let’s start by looking at it graphically. If we start with our regression model looking at the relationship between voting and age, we can calculate a residual for each data point, which is the difference between the data point in question and the line of best fit. We can then plot those residuals against the percentage of graduates. What we are now plotting is the voting patterns adjusted for age. So if we see a relationship with the percent of graduates, then we know that it’s still an independent predictor after adjusting for age.
This is what we get if we do that:
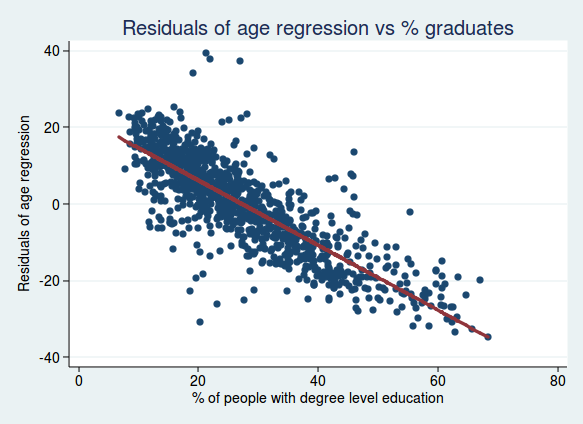
As you can see, it’s still a very strong relationship, so we can conclude that the percentage of graduates is a good predictor of voting, even after taking account of age.
What if we take account of both age and ethnicity? Here’s what we get if we do the same analysis but with the residuals from an analysis of both age and ethnicity:
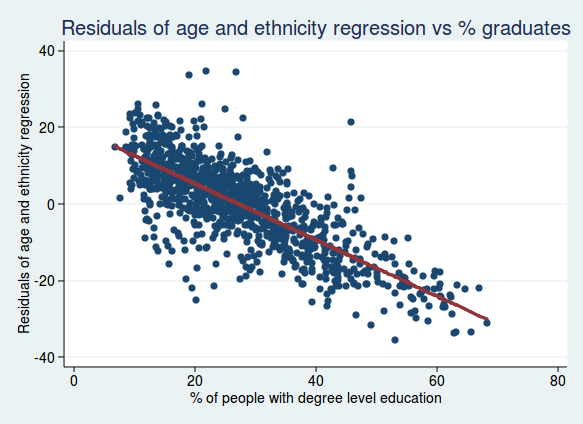
Again, the relationship still seems very strong, so the percentage of graduates really does seem to be a robust independent predictor of voting.
For the more statistically minded, another way of looking at this is to look at the regression coefficient for the percentage of graduates alone, or after adjusting for age and ethnicity (in all cases with the % voting leave as the dependent variable). Here is what we get:
| Model |
Regression cofficient |
t |
P value |
| Education alone |
-0.97 |
-45.9 |
< 0.001 |
| Education and age |
-0.90 |
-52.5 |
< 0.001 |
| Education and ethnicity |
-0.91 |
-55.0 |
< 0.001 |
| Education, age, and ethnicity |
-0.89 |
-53.9 |
< 0.001 |
So although the regression coefficient does get slightly smaller after adjusting for age and ethnicity, it doesn’t get much smaller, and remains highly statistically significant.
What if we turn this on its head and ask whether age is still an important predictor after adjusting for education?
Here is a graph of the residuals from the analysis of voting and education, plotted against age:
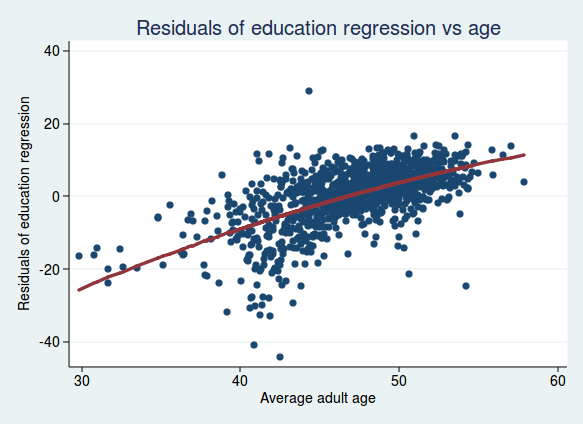
There is still a clear relationship, though perhaps not quite as strong as before. And what if we look at the residuals adjusted for both education and ethnicity, plotted against age?
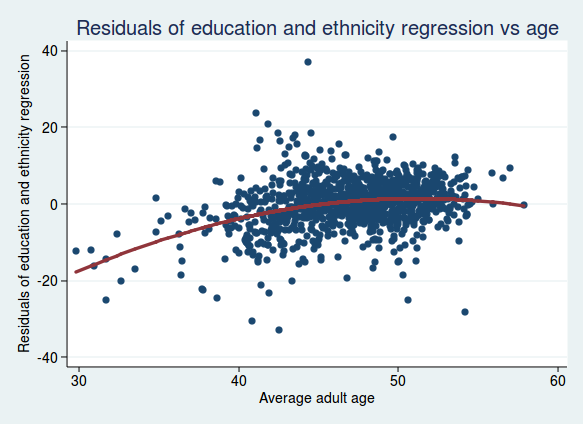
The relationship seems to be flattening out, so maybe age isn’t such a strong independent predictor once we take account of education and ethnicity (it turns out that areas with a higher proportion of white people also tend to be older).
For the statistically minded, here are what the regression coefficients look like (for ease of interpretation, I’m not using a quadratic term for age here and only looking at the linear relationship with age).
| Model |
Regression cofficient |
t |
P value |
| Age alone |
1.66 |
17.2 |
< 0.001 |
| Age and education |
1.28 |
25.3 |
< 0.001 |
| Age and ethnicity |
0.71 |
5.95 |
< 0.001 |
| Age, education, and ethnicity |
0.82 |
13.5 |
< 0.001 |
Here the adjusted regression coefficient is considerably smaller than the unadjusted one, showing that the initially strong looking relationship with age isn’t quite as strong as it seems once we take account of education and ethnicity.
So after all this I think it is safe to conclude that education is a remarkably strong predictor of voting outcome in the EU referendum, and that that relationship is not much affected by age or ethnicity. On the other hand, the relationship between age and voting outcome, while still certainly strong and statistically significant, is not quite as strong as it first appears before education and ethnicity are taken into account.
One important caveat with all these analyses of course is that they are based on aggregate data for electoral wards rather than individual data, so they may be subject to the ecological fallacy. We know that wards with a high percentage of graduates are more likely to have voted remain, but we don’t know whether individuals with degrees are more likely to have voted remain. It seems reasonably likely that that would also be true, but we can’t conclude it with certainty from the data here.
Another caveat is that data were not available from all electoral wards, and the analysis above is based on a subset of 1070 wards in England only (there are 8750 wards in England and Wales). However, the average percent voting leave in the sample analysed here was 52%, so it seems that it is probably broadly representative of the national picture.
All of this of course raises the question of why wards with a higher proportion of graduates were less likely to vote leave, but that’s probably a question for another day, unless you want to have a go at answering it in the comments.
Update 12 February 2017:
Since I posted this yesterday, I have done some further analysis, this time looking at the effect of socioeconomic classification. This classifies people according to the socioeconomic status (SES) of the job they do, ranging from 1 (higher managerial and professional occupations) to 8 (long term unemployed).
I thought it would be interesting to see the extent to which education was a marker for socioeconomic status. Perhaps it’s not really having a degree level education that predicts voting remain, but it’s being in a higher socioeconomic group?
To get a single number I could use for socioeconomic status, I calculated the percentage of people in each ward in categories 1 and 2 (the highest status categories). (I also repeated the analysis calculating the average status for each ward, and the conclusions were essentially the same, so I’m not presenting those results here.)
The relationship between socioeconomic status and voting leave looks like this:
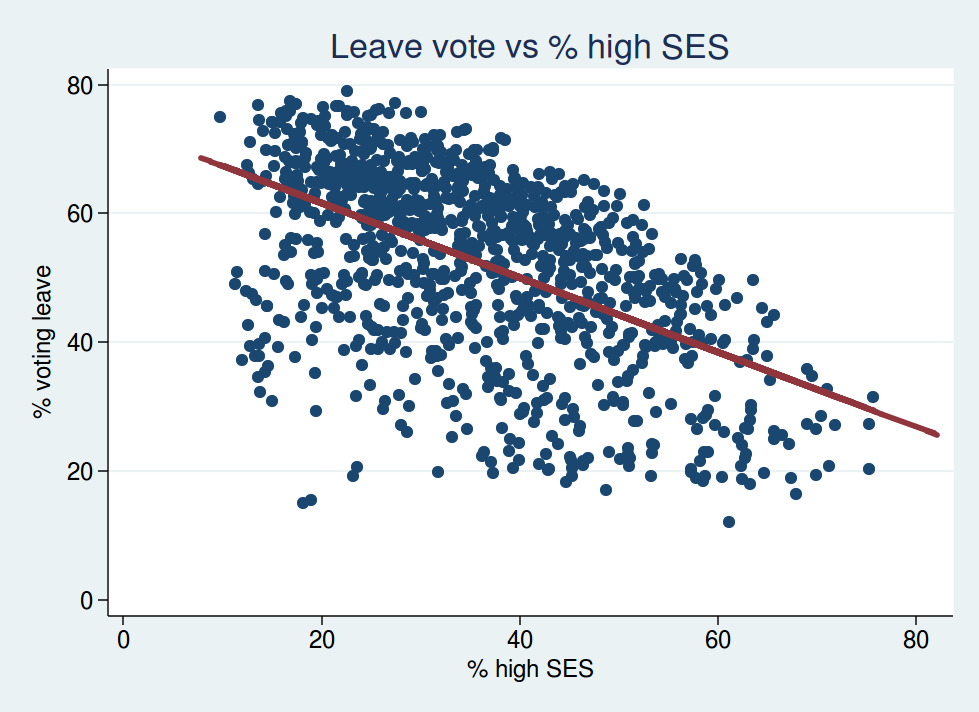
This shouldn’t come as a surprise. Wards with more people in higher SES groups were less likely to vote leave. That fits with what you would expect from the education data: wards with more people with higher SES are probably also those with more graduates.
However, if we look at the multivariable analyses, this is where it starts to get interesting.
Let’s look at the residuals from the analysis of education plotted against SES. This shows the relationship between voting leave and SES after adjusting for education.
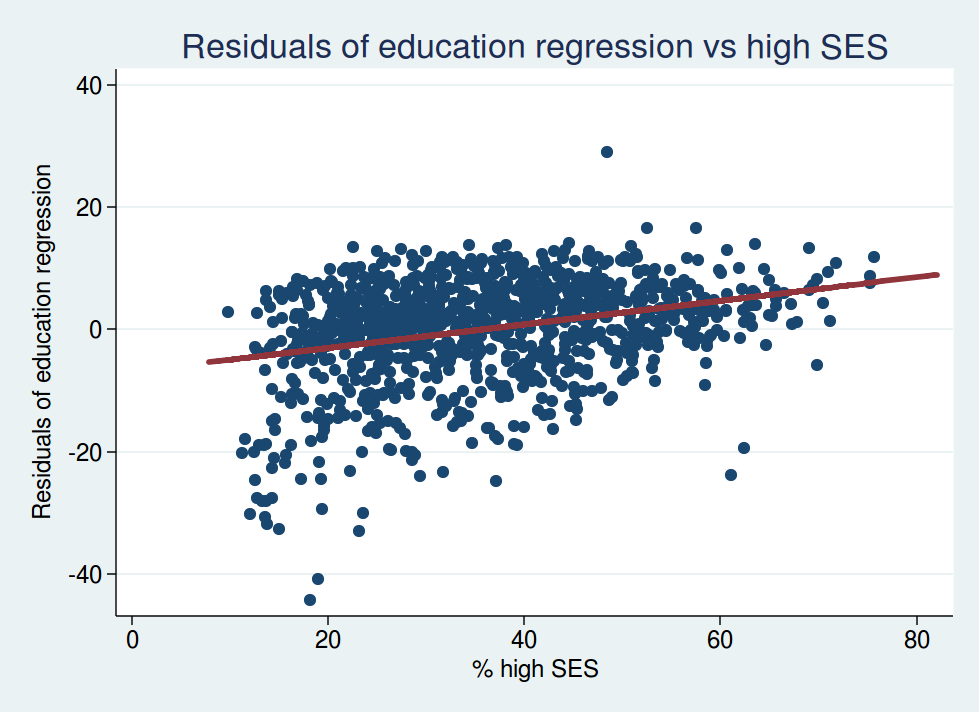
You’ll note that the slope of the best-fit regression line is now going the other way: it now slopes upwards instead of downwards. This tells us that, for wards with identical proportions of graduates, the ones with higher SES are now more likely to vote leave.
So what we are seeing here is most definitely a correlation between education and voting behaviour. Other things (ie education) being equal, wards with a higher proportion of people in high SES categories were more likely to vote leave.
For the statistically minded, here is what the regression coefficients look like. Here are the regression coefficients for the effect of socioeconomic status on voting leave:
| Model |
Regression cofficient |
t |
P value |
| SES alone |
-0.58 |
-20.6 |
< 0.001 |
| SES and education |
0.81 |
26.5 |
< 0.001 |
| SES, education, and ethnicity |
0.49 |
12.4 |
< 0.001 |
| SES, education, age, and ethnicity |
0.31 |
6.5 |
< 0.001 |
Note how the sign of the regression coefficient reverses in the adjusted analyses, consistent with the slope in the graph changing from downward sloping to upward sloping.
And what happens to the regression coefficients for education once we adjust for SES?
| Model |
Regression cofficient |
t |
P value |
| Education alone |
-0.97 |
-45.9 |
< 0.001 |
| Education and SES |
-1.75 |
-51.9 |
< 0.001 |
| Education, SES, age, and ethnicity |
-1.20 |
-23.4 |
< 0.001 |
Here the relationship between education and voting remain becomes even stronger after adjusting for SES. This shows us that it really is education that is correlated with voting behaviour, and it’s not simply a marker for higher SES. In fact once you adjust for education, higher SES predicts a greater likelihood of voting leave.
To be honest, I’m not sure these results are what I expected to see. I think it’s worth reiterating the caveat above about the ecological fallacy. We do not know whether individuals of higher socioeconomic status are more likely to vote leave after adjusting for education. All we can say is that electoral wards with a higher proportion of people of high SES are more likely to vote leave after adjusting for the proportion of people in that ward with degree level education.
But with those caveats in mind, it certainly seems as if it is a more educated population first and foremost which predicts a higher remain vote, and not a population of higher socioeconomic status.